Основные понятия теории вероятности в теории риска

Под вероятностью случайного события р(А) понимают частоту его появления в полной совокупности событий: Р(А)=m/n   (1),
 где m – число благоприятствующих событию исходов; n – общее число исходов.

Теорема сложения. Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного появления:

             p(А+В) = p(А) + p(В) – p(А/В)       (2)

Если события  А и В несовместны, то p(А+В) = p(А) + p(В)   (3)

Условной вероятностью p(A/B) называют вероятность события А, вычисленную в предположении, что событие В уже наступило.

Теорема умножения. Вероятность совместного наступления двух событий равна вероятности одного из них, умноженной на условную вероятность другого при условии, что первое событие наступило: p(AB)=p(A)p(A/B)     (4)

Если события А и В независимы, то p(AB)=p(A)p(B)            (5)

Пусть вероятность события А равна р. Тогда вероятность противоположного события равна (1- р), которую обычно обозначают через q. Если вероятность р характеризует выигрыш, то вероятность q – степень риска.

Вероятность того, что в n независимых и одинаковых испытаниях успех наступит m раз, выражается формулой Бернулли: 

                                        (6)

где р – вероятность появления успеха в каждом испытании; q=1-p – вероятность неудачи.

Формула полной вероятности позволяет вычислить вероятность интересующего события через его условные вероятности в предположении неких гипотез, а также вероятностей этих гипотез.

Если событие А может наступить только при появлении одного из несовместных событий (гипотез) , то вероятность события А вычисляется по формуле полной вероятности:                (7)

где  p(H_i)- вероятность гипотезы Н_i; p(A\H_i)  - условная вероятность события А при этой гипотезе.

Если до опыта вероятности гипотез были 

 , а в результате опыта появилось событие А, то с учетом этого события “новые”, т.е. условные, вероятности гипотез вычисляются по формуле Байеса:

(8)

 где Р(А)  - полная вероятность события А.

В схемах оценки риска широко применим аппарат случайных величин. Случайной называют величину (СВ), которая в результате испытания принимает только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Дискретные случайные величины задают законом распределения, таблицей возможных значений х₁, х₂,…,х_n с указанием вероятностей их появления р₁, р₂,…, р_n.

Характеристикой среднего значения случайной величины служит математическое ожидание: 

       (9)

Характеристиками рассеяния возможных значений случайной величины отностительно математического ожидания служат дисперсия и среднее квадратическое отклонение. Дисперсией случайной величины  называют математическое ожидание квадрата ее отклонения от ее математического ожидания: 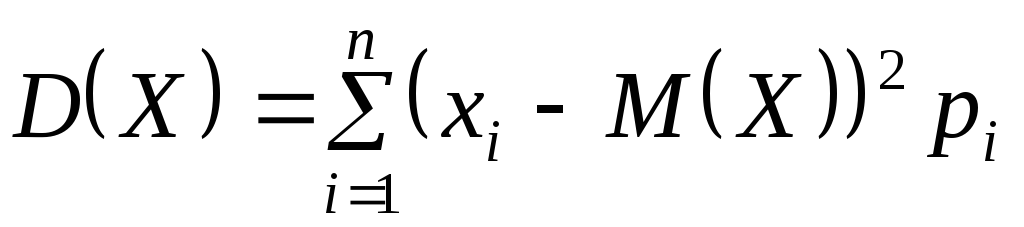                                   (10)

Размерность дисперсии случайной величины равна квадрату размерности самой величины, поэтому на практике удобно пользоваться квадратным корнем из дисперсии. Эта характеристика имеет ту же размерность, что и величина, и называется средним квадратическим отклонением СВ: 

  (11).

В теории принятия решений в условиях неопределенности справедлив критерий: чем больше среднеквадратическое отклонение при приближенно равных математических ожиданиях, тем степень риска больше.